近日,江苏省应用数学科学研究中心虞文武教授团队在因果发现领域解决了由于马尔科夫等价类存在导致的因果结构无法唯一准确识别的难题,揭示了唯一因果网络的时空高阶形式,证明了因果发现的唯一性原理与可分解性性质,提出了高维耦合动态系统的唯一因果发现算法。这两项成果分别发表在《IEEE Transactions on Artificial Intelligence》和《IEEE Transactions on Network Science and Engineering》期刊上,为复杂系统的时空因果推断提供了全新的理论依据。
因果发现作为复杂系统认知和人工智能可解释性研究的重要组成环节,是数学基础理论与人工智能研究的热门方向,也是经济、管理、信息、医学等领域广泛使用的技术手段。马尔科夫等价类的存在制约了因果发现的收敛性与准确性,是当今因果发现领域面临的主要瓶颈挑战之一。如图1所示,给定任意的三个变量,从数据中只能推断出该三元组具有相同的条件独立性或不确定性,无法进一步区分两种链式结构和一种分叉结构,从而造成这三种网络结构属于马尔可夫等价类。这种马尔可夫等价类的存在使得因果网络的结构不收敛不唯一,导致无法进一步进行有效的干预和反事实推理。
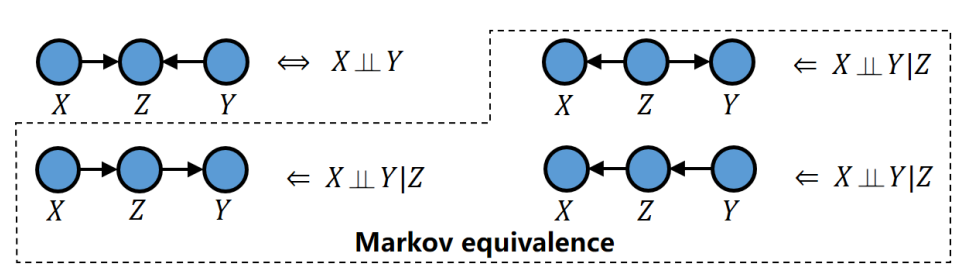
图:马尔科夫等价类问题
为了解决此难题,虞文武教授团队从信息传递的角度出发,提出了唯一因果网络模型(Unique Causal Network, UCN),考虑了变量间因果影响的时滞关系,引入了信息路径阻塞的概念,从而解释了网络结构中链式结构的消失,最终严格证明了UCN的唯一性。进一步的,团队揭示了UCN的分布式可解耦性质,将算法缩短至多项式时间复杂度。UCN具备唯一推断因果网络结构的特性,将因果发现领域的研究推广到时空高阶的形式。
此外,在高维耦合动态系统的因果发现领域,团队提出了一种神经因果熵算法,设计了两个关键估计器——高维双变量互信息神经估计器和高维条件互信息神经估计器,以准确估计高维系统中的因果熵。这一算法在高维实证时空数据场景下能够准确推断出多变量间的因果关系。
这两项研究成果获得中心课题“复杂系统的无偏高阶高维因果推断”(课题负责人:陈都鑫)的支持,不仅在基础理论上推动了因果发现研究的进展,还在复杂系统任务中展现了广阔的应用前景,为智能通信、智能交通、医工交叉等复杂系统的耦合结构认知夯实了理论基础。
文章链接:
https://xplorestaging.ieee.org/document/10723109
https://xplorestaging.ieee.org/document/10716792

