该研究针对典型的离散时间与状态动力学系统,给出了基于节点染色图理论的分析与设计框架,并设计了一系列程序化的多项式时间内可执行的能观性与能检测性判别算法,可用于逻辑网络、符号动力学、离散事件系统和Markov链等相关研究。在基因调控网络的研究中,通过定义结构等价性提出了逻辑网络强结构能镇定/结构能控/结构能观的概念,所建立的充要判据计算复杂度仅与网络节点数多项式相关。在此基础上,网络的最少节点控制问题被显式地解决。针对网络动力学已知时逻辑网络存在的维数灾难问题,利用网络拓扑中的激活-抑制信息,成功地设计了适用于大规模逻辑网络的分布式牵制控制策略,从理论层面揭示了F.J. Muller等在《Cell》2011中所观察到的实验现象背后的机理。主要结果已以Full Paper形式发表在《IEEE Trans. Automatic Control》,部分成果入选2023年度“基础研究领域”十大科技进展(完成人:卢剑权,曹进德,朱诗勇,林琳)。
所建立的离散时间与状态动力学系统的分析与控制框架可以帮助科学家们更好地理解基因调控网络的运作原理和动态行为。通过对基因调控网络进行模拟和分析,研究者们可以揭示基因调控过程中的关键因素和机制,从而为疾病治疗和基因工程等领域提供更准确的指导和方法。其次,逻辑网络的强结构能镇定定义和分布式牵制控制策略的设计为基因调控提供了新的思路和方法,更有助于实现对基因表达的精确控制。这对于疾病治疗、基因修复和生物合成等领域具有重要意义,有望为相关领域的研究和应用带来新的突破和进展。
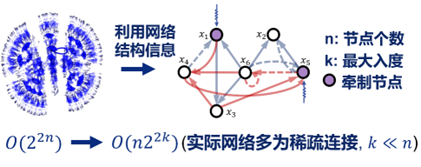
图1:控制器的设计复杂度仅与网络节点的最大入度指数相关
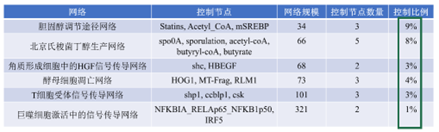
图2:理论结果在真实网络中的验证

